https://doi.org/10.1140/epjp/s13360-023-03888-4
Regular Article
Linear and nonlinear stability analyses of double-diffusive convection in a porous layer due to magnetic field and throughflow effects
Department of Mathematics, National Institute of Technology Warangal, 506004, Hanamkonda, Warangal, TS, India
Received:
2
January
2023
Accepted:
7
March
2023
Published online:
24
March
2023
This study has looked into the beginning of double-diffusive convection in a horizontal fluid-saturated porous layer for both linear and nonlinear cases. Vertical throughflow and the magnetic field effects are taken into consideration during the investigation. The normal mode technique and the energy method are, respectively, employed to analyze the linear and nonlinear stability. The corresponding linear and nonlinear eigenvalue equations were solved numerically via boundary value problem solver bvp4c routine in MATLAB (2022a). The critical thermal Rayleigh number and associated wave number are obtained for various flow-governing parameters and shown them graphically. It has been noticed that the system shows more stableness for higher values of magnetic parameter (
) and helps to compress the subcritical instabilities region. Increasing the Lewis number (Le) stabilized the fluid motion while the system is destabilized at a high solutal Rayleigh number (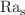
). Further, the significant impact of the Pèclet number (Pe) on the instability mechanism is discussed due to upward or downward throughflow whether a magnetic field is present or not.
P. Barman, D. Srinivasachrya, D. Barman have contributed equally to this work.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
