https://doi.org/10.1140/epjp/s13360-024-05207-x
Regular Article
Analyzing the topography of thermosolutal rotating convection of a Casson fluid in a sparsely packed porous channel
Department of Mathematics, National Institute of Technology Warangal, Telangana, India
Received:
25
November
2023
Accepted:
18
April
2024
Published online:
13
May
2024
This paper discusses the thermosolutal rotating convection of a Casson fluid in a sparsely packed porous channel with variable boundaries. For linear analyses, the normal mode method is utilized to solve the governing equations. The system of equations are solved using a one-term Galerkin method for finding critical Rayleigh number. Meanwhile, the eigenvalue problem is numerically solved using the Chebyshev collocation method. Graphical representations are provided of the effects of the Casson fluid (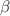
) and separation parameters (
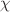) on velocity, temperature, and solute concentration profiles for fixed parameter values of Rayleigh number (R), Darcy number (Da), and Taylor number (Ta). Influence of Casson fluid and separation parameters is demonstrated for the system growth rate, stability curves, and critical boundary conditions. However, it turns out that the Darcy number, Taylor number, Lewis number, and Prandtl number all stabilize the system in an unsteady flow. Multiple-scale analysis is used to develop the coupled Landau–Ginzburg equation in weakly nonlinear theory. Furthermore, the study develops amplitude cellular convections in a stability region.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
