Eur. Phys. J. Plus (2021) 136: 795
https://doi.org/10.1140/epjp/s13360-021-01736-x

Regular Article

Weakly nonlinear thermohaline convection in a sparsely packed porous medium due to horizontal magnetic field

¹ Department of Mathematics, National Institute of Technology Warangal, 506004, Warangal, India
² Department of HBS, Godavari Institute of Engineering and Technology, 533296, Rajahmundry, Andhra Pradesh, India

^a benerji77@gmail.com

Received: 17 March 2021
Accepted: 5 July 2021
Published online: 2 August 2021

Abstract

Thermohaline convection in a sparsely packed porous medium is studied due to horizontal magnetic field, using both linear and weakly nonlinear stability analyses. The Darcy–Lapwood–Brinkman (DLB) model is employed as the momentum equation. In the linear stability analysis, the normal mode technique is used to find the thermal critical Rayleigh number which is a function of q, Da, 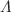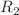$\mathrm{\Lambda }$, $R_2$ and L. In the weakly nonlinear analysis, a nonlinear two-dimensional Landau–Ginzburg (LG) equation is derived at the onset of stationary convection and the secondary instabilities and heat transport by convection are studied. Coupled one-dimensional LG equations are derived at the onset of oscillatory convection, and the stability regions of steady state, standing waves and travelling waves are studied.