https://doi.org/10.1140/epjp/s13360-024-05427-1
Regular Article
Study of double-diffusive gravity modulated biothermal convection in porous media under internal heating effect
1
Department of Studies and Research in Mathematics, Tumkur University, 572103, Tumakuru, India
2
Chaitanya Bharathi Institute of Technology, 500075, Hyderabad, Telangana, India
3
Faculty of Engineering, Kuwait College of Science and Technology, 35004, Doha, Kuwait
Received:
19
April
2024
Accepted:
3
July
2024
Published online:
17
July
2024
Double diffusion combined with thermo-bioconvection in porous media under two prominent effects such as gravity modulation and internal heating are considered in the present work. The impact of considering double diffusion and porous medium in the current problem is studied graphically. We deal with linear and weakly nonlinear theory of the system. Linear theory helps in the analysis of onset of convection. The stability of the system is also discussed in this section. Onset of convection is governed by critical(threshold) Rayleigh number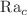 
. The marginal stability curves are plotted between critical Rayleigh number and wavenumber for all the parameters that exist in the study which helps in analyzing the stability of the system. Weakly nonlinear stability analysis is carried out to study heat and mass transfer in the system. Due to the gravity modulation, there arise amplitude and frequency for the corresponding fluid under convection. From such nonlinear study, we arrive at an amplitude equation called Ginzburg–Landau (GL) equation. Further, on solving GL equation, we discuss heat and mass transfer in terms of Nusselt number Nu and Sherwood number Sh. The graphical study of heat and mass transfer is performed by plotting Nu versus time scale 
and Sh against , respectively, for various parameters existing in the study. The convection cells arise due to temperature difference between the horizontal plates are shown in the form of streamlines and isotherms.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
