https://doi.org/10.1140/epjp/s13360-025-06547-y
Regular Article
Construction of Schrödinger, Pauli and Dirac equations from Vlasov equation in case of Lorenz gauge
1
Faculty of Physics, Lomonosov Moscow State University, 119991, Moscow, Russia
2
Moscow Technical University of Communications and Informatics, 123423, Moscow, Russia
3
Dubna State University, Moscow Region, 141980, Dubna, Russia
4
Joint Institute for Nuclear Research, Moscow Region, 141980, Dubna, Russia
Received:
18
February
2025
Accepted:
9
June
2025
Published online:
2
July
2025
The Madelung representation for the wave function makes it possible to transform the Schrödinger equation into the Hamilton–Jacobi equation and the continuity equation (the first Vlasov equation). In the present paper, the opposite transformation is mathematically rigorously shown, that is the extended analogues of the Schrödinger and Hamilton–Jacobi equations, as well as the Pauli, Dirac, and Maxwell equations, can be obtained from the continuity equation. We have succeeded to derive an analogue of the Schrödinger equation which differs fundamentally from the well-known Schrödinger equation by the presence of “mixed” electromagnetic fields containing both the classical Maxwell fields and probabilistic fields, which are obtained by introducing a new—Lorenz gauge and the principle of self-consistency. In addition to the relation between the vector and scalar potentials for classical electromagnetic fields, the new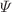 
-gauge provides a connection between the quantum scalar and vector potentials, which are purely statistical in nature. It is shown that if the conditions of self-consistency are met then the analogues of the Maxwell equations are valid for such new statistical “electromagnetic” fields, but with probabilistic charges and currents.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
