https://doi.org/10.1140/epjp/s13360-025-06171-w
Regular Article
Uncovering the soliton solutions and interaction aspects of combined CBS-nCBS model utilizing Bäcklund transform
1
Department of Mathematics, University of the Punjab, Quaid-e-Azam Campus, Lahore, Pakistan
2
School of Electrical and Electronic Engineering, Nanyang Technological University, 639798, Singapore, Singapore
3
Department of Mathematics, College of Science, King Khalid University, 61413, Abha, Saudi Arabia
4
Department of Computer Engineering, Biruni University, 34010, Istanbul, Turkey
Received:
19
December
2024
Accepted:
23
February
2025
Published online:
17
March
2025
The Calogero-Bogoyavlenskii-Schiff (CBS) equation is a nonlinear integrable partial differential equation that plays a significant role in studying solitons, wave interactions, and various physical phenomena, including fluid dynamics and optical fibers. This work focuses on solving the (3+1)-dimensional combined CBS-negative-order CBS (CBS-nCBS) equation using multiple analytical techniques. First, the Hirota bilinear form is employed to derive the Bäcklund transformation through different exchange identities. This transformation yields exponential and rational function solutions, enabling the identification of singular and kink solitons. Additionally, by applying various ansatzes within the bilinear framework, we construct two-wave, three-wave, multi-wave, and breather solutions, providing deeper insights into the equation’s characteristics. Furthermore, the given model is transformed into an ordinary differential equation via a traveling wave transformation. The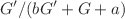 
method is then applied to extract solutions involving trigonometric and hyperbolic functions, leading to periodic and kink solitons. The graphical representations presented in this study are instrumental in visualizing the intricate dynamics of these solutions. The findings enhance our understanding of the diverse soliton structures and broaden the potential applications of the CBS equation.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
