https://doi.org/10.1140/epjp/s13360-025-06273-5
Regular Article
Integrability aspects, Wronskian solution, Grammian solution, lump and lump-multi-kink solutions of an extended 
-dimensional Bogoyavlensky-Konopelchenko equation
1
Department of Mathematics, School of Computer Science and Artificial Intelligence, SR University, 506371, Warangal, Telangana, India
2
Department of Mathematics, University of Kalyani, 741235, Kalyani, India
3
Department of Mathematics, Zhejiang Normal University, 321004, Jinhua, Zhejiang, China
4
Department of Mathematics, King Abdulaziz University, 21589, Jeddah, Saudi Arabia
5
Department of Mathematics and Statistics, University of South Florida, 33620-5700, Tampa, FL, USA
6
Material Science Innovation and Modelling, North-West University Mafikeng Campus, Private Bag X2046, 2735, Mmabatho, South Africa
a
mawx@cas.usf.edu
b amiya620@gmail.com, amiyamath18@klyuniv.ac.in
Received:
17
November
2024
Accepted:
27
March
2025
Published online:
13
May
2025
In this article, we examine an extended -dimensional Bogoyavlensky-Konopelchenko equation, which models the interaction between a Riemann wave and a long wave in a fluid. This equation has significant applications in the study of shallow-water waves, ion-acoustic waves, and water propagation in liquids. We explore the integrability of this model through various approaches. First, we derive the Hirota bilinear form using the Bell polynomial theory. By decoupling the two-field condition, we calculate the bilinear Bäcklund transformation. Subsequently, through the Cole–Hopf transformation and the linearization of the Bäcklund transformation, we obtain the Lax pair. Additionally, we derive infinitely many conservation laws using Bell polynomial theory. We compute one-, two-, and three-soliton solutions directly from the Hirota bilinear form and present their 3-D plot, density plot and 2D plot graphically. We establish the Wronskian condition by employing the Plücker relation, ensuring that the N-soliton solutions of the equation can be represented as Wronskian determinants. Additionally, the use of a suitable transformation and the Wronskian determinant condition in our model establishes the widely known Wronskian solution to the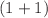 
-dimensional KdV equation. We derive a rational Wronskian solution by selecting a specific coefficient matrix in the resulting Wronskian formulation. Furthermore, we calculate one-, two-, and three-soliton solutions in Wronskian form and visually depict their soliton dynamics using Mathematica with appropriately chosen parameters. Additionally, we present a Grammian determinant solution, utilizing the Jacobi relation. To obtain the lump solution, we employ a quadratic function as a test function within the Hirota bilinear form. Furthermore, we calculate two sets of lump-multi-kink solutions employing two distinct test functions. We provide a visual comparison of the evolutionary dynamics of the lump-multi-kink solutions corresponding to two distinct test functions.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
