https://doi.org/10.1140/epjp/s13360-022-02880-8
Regular Article
Reflection of inhomogeneous plane waves at the surface of an unsaturated porothermoelastic media
1
Department of Mathematics, M P College for Women, Mandi Dabwali, 125104, Sirsa, Haryana, India
2
Department of Mathematics, Dr. B R Ambedkar Govt. College, Dabwali, 125104, Sirsa, Haryana, India
3
Department of Mathematics, Shri JJT University, Chudela, Vidyanagari, 333010, Jhunjhunu, Rajasthan, India
Received:
5
April
2022
Accepted:
25
May
2022
Published online:
25
June
2022
A generalized porothermoelasticity theory developed by Wang et al. (IEEE Trans Geosci Remote Sens 60:1–14, 2021) for plane wave propagation in an unsaturated porothermoelastic media is employed in this study. This theory incorporates LS (Lord–Shulman) and GL (Green–Lindsay) theories. The generalized equations of motions are solved using the potential functions approach and predict the four dilatational waves and one shear wave. The incidence of the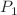 
(or SV) wave generates the five reflected waves. The suitable potentials for the incident and reflected waves are considered, which meet the necessary boundary constraints with the aid of Snell’s law. The reflection coefficients are computed as a system of five linear non-homogeneous equations based on the permeable and impermeable boundary constrains. The partitioning of incident energy is then computed using these reflection coefficients. The mathematical derivations introduced in this study can investigate the impact of subsurface features (liquid saturation, porosity, surface pores characteristics, thermal expansion coefficients, wave frequency) on the propagation characteristics (propagation and attenuation directions, phase shift, energy ratio) of reflected waves. In addition, the propagation characteristics for LS (Lord–Shulman) and GL (Green–Lindsay) theories, and permeable and impermeable boundary constraints are compared numerically. Moreover, energy conservation is also verified at the stress-free surface of unsaturated porothermoelastic media.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2022
