https://doi.org/10.1140/epjp/s13360-024-05797-6
Regular Article
Kinetic theory of stellar systems and two-dimensional vortices
Laboratoire de Physique Théorique, Université de Toulouse, CNRS, UPS, Toulouse, France
Received:
1
June
2024
Accepted:
4
November
2024
Published online:
24
December
2024
We discuss the kinetic theory of stellar systems and two-dimensional vortices and stress their analogies. We recall the derivation of the Landau and Lenard–Balescu equations from the Klimontovich formalism. These equations take into account two-body correlations and are valid at the order 1/N, where N is the number of particles in the system. They have the structure of a Fokker–Planck equation involving a diffusion term and a drift term. The systematic drift of a vortex is the counterpart of the dynamical friction experienced by a star. At equilibrium, the diffusion and the drift terms balance each other establishing the Boltzmann distribution of statistical mechanics. We discuss the problem of kinetic blocking in certain cases and how it can be solved at the order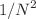 
by the consideration of three-body correlations. We also consider the behaviour of the system close to the critical point following a recent suggestion by Hamilton and Heinemann (2023). We present a simple calculation, valid for spatially homogeneous systems with long-range interactions described by the Cauchy distribution, showing how the consideration of the Landau modes regularizes the divergence of the friction by polarization at the critical point. We mention, however, that fluctuations may be very important close to the critical point and that deterministic kinetic equations for the mean distribution function (such as the Landau and Lenard–Balescu equations) should be replaced by stochastic kinetic equations.
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
