https://doi.org/10.1140/epjp/s13360-023-04030-0
Regular Article
Arbitrary 
-state solutions of the Klein–Gordon equation with the Eckart plus a class of Yukawa potential and its non-relativistic thermal properties
1
Department of Physics, Karadeniz Technical University, 61080, Trabzon, Turkey
2
Department of Physics, Middle East Technical University, 06800, Ankara, Turkey
Received:
12
January
2023
Accepted:
29
April
2023
Published online:
14
May
2023
We report bound-state solutions of the Klein–Gordon equation with a novel combined potential, the Eckart plus a class of Yukawa potential, by means of the parametric Nikiforov–Uvarov method. To deal the centrifugal and the coulombic behavior terms, we apply the Greene–Aldrich approximation scheme. We present any -state energy eigenvalues and the corresponding normalized wave functions of a mentioned system in a closed form. We discuss various special cases related to our considered potential which are utility for other physical systems and show that these are consistent with previous reports in literature. Moreover, we calculate the non-relativistic thermodynamic quantities (partition function, mean energy, free energy, specific heat and entropy) for the potential model in question, and investigate them for a few diatomic molecules. We find that the energy eigenvalues are sensitive with regard to the quantum numbers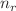 
and as well as the parameter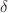 
. Our results show that energy eigenvalues are more bounded at either smaller quantum number or smaller parameter .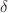
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
