https://doi.org/10.1140/epjp/s13360-023-03715-w
Regular Article
Bound state solutions of the Klein–Gordon equation under a non-central potential: the Eckart plus a ring-shaped potential
1
Department of Theoretical Physics, Baku State University, Z. Khalilov St. 23, 1148, Baku, Azerbaijan
2
Department of Physics, Karadeniz Technical University, TR61080, Trabzon, Turkey
3
Institute for Physical Problems, Baku State University, Z. Khalilov St. 23, 1148, Baku, Azerbaijan
4
Department of Physics, University of Wisconsin-Madison, 53706, Madison, WI, USA
5
Azerbaijan State University of Economics, Istiqlaliyyat St. 6, 1001, Baku, Azerbaijan
Received:
5
December
2022
Accepted:
17
January
2023
Published online:
28
January
2023
We report the bound state solutions of a novel non-central potential, the Eckart plus a ring-shaped potential, in the Klein–Gordon equation by using the Nikiforov–Uvarov method. We apply a developed scheme to overcome the centrifugal term. The energy eigenvalues and the corresponding normalised wave function of a mentioned system are presented in a closed and compact form. We also discuss various special cases related to our considered potential which are utility for other physical systems, consistent with previous studies. We then compute the eigenvalues and eigenfunctions numerically for arbitrary quantum numbers to show the accuracy of our results. It is shown that our results are sensitive to the parameter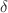 
as well as the quantum numbers 
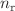and N or l, as expected.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
