Eur. Phys. J. Plus (2021) 136: 244
https://doi.org/10.1140/epjp/s13360-021-01202-8

Regular Article

Generalized tanh-shaped hyperbolic potential: bound state solution of Schrödinger equation

¹ Department of Equations of Mathematical Physics, Baku State University, 1148, Baku, Azerbaijan
² Department of Chemistry and Physics, Lankaran State University, 4200, Lankaran, Azerbaijan
³ Institute of Applied Mathematics, Baku State University, 1148, Baku, Azerbaijan
⁴ Institute for Physical Problems, Baku State University, 1148, Baku, Azerbaijan

^d badalovvatan@yahoo.com

Received: 4 December 2020
Accepted: 6 February 2021
Published online: 22 February 2021

Abstract

The development of potential theory offers compelling coarse-grained descriptions of fundamental interactions in quantum field theory. In this paper, we propose 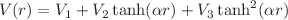$V(r)=V_1+V_{2}tanh(\alpha r)+V_3{tanh}^2(\alpha r)$ generalized tanh-shaped hyperbolic potential, which in itself contains several important physical potentials. Next, we present the bound state solution of the modified radial Schrödinger equation with this potential by using the Nikiforov–Uvarov method. The obtained energy eigenvalues and corresponding radial wave functions are expressed in terms of the Jacobi polynomials for arbitrary l states. It is also shown that the energy eigenvalues are sensitively associated with potential parameters for quantum states. The generalized tanh-shaped hyperbolic potential and its obtained energy eigenvalues are in excellent overlap with the already reported results in some instances. Altogether, the potential model is predicted to be a possible candidate for prescribing multiple quantum systems simultaneously.