Eur. Phys. J. Plus (2021) 136: 208
https://doi.org/10.1140/epjp/s13360-021-01163-y

Regular Article

Analytical bound state solutions of the Dirac equation with the Hulthén plus a class of Yukawa potential including a Coulomb-like tensor interaction

¹ Department of Theoretical Physics, Baku State University, Z. Khalilov st. 23, AZ1148, Baku, Azerbaijan
² Department of Physics, Karadeniz Technical University, TR61080, Trabzon, Turkey
³ Institute for Physical Problems, Baku State University, Z. Khalilov st. 23, AZ1148, Baku, Azerbaijan
⁴ Azerbaijan State University of Economics, Istiqlaliyyat st.6, AZ1001, Baku, Azerbaijan

^b mehmetdemirci@ktu.edu.tr

Received: 15 October 2020
Accepted: 27 January 2021
Published online: 13 February 2021

Abstract

We examine the bound state solutions of the Dirac equation under the spin and pseudospin symmetries for a new suggested combined potential, Hulthén plus a class of Yukawa potential including a Coulomb-like tensor interaction. An improved scheme is employed to deal with the centrifugal (pseudocentrifugal) term. Using the Nikiforov–Uvarov and SUSYQM methods, we analytically develop the relativistic energy eigenvalues and associated Dirac spinor components of wave functions. We find that both methods give entirely the same results. Modification of our results to fit some particular potentials, which are useful in some other systems, is also discussed. We obtain complete agreement with the findings of previous works. The spin and pseudospin bound state energy spectra for various levels are presented in the absence as well as the presence of tensor coupling. Both energy spectrums are sensitive with regard to the quantum numbers $\kappa$ and n, as well as the parameter $\delta$. 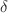We also notice that the degeneracies between Dirac spin and pseudospin-doublet eigenstate partners are completely removed by the tensor interaction. 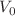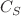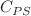Finally, we present the parameter space of allowable bound state regions of potential strength $V_0$ with constants $C_S$ and $C_{\mathit{PS}}$ for both symmetry limits.