Eur. Phys. J. Plus (2022) 137: 1282
https://doi.org/10.1140/epjp/s13360-022-03482-0

Regular Article

Robustness of Tsallis statistics to describe relativistic electrons in Hartmann potential

¹ Department of Physics, Ahvaz Branch, Islamic Azad University, Ahvaz, Iran
² Physics Department, Shahrood University, P. O. Box 3619995161-316, Shahrood, Iran

^b behzadlari1979@gmail.com

Received: 29 August 2022
Accepted: 11 November 2022
Published online: 27 November 2022

Abstract

We consider a relativistic particle in spherical Hartmann potential. Using Tsallis statistics, we investigate the convexity and concavity of the deformed partition function and other thermodynamics properties of the system. We propose an upper bound to calculate the partition function that satisfies the Tsallis conditions. In the case of Tsallis statistics (based on gamma distribution), we find that the 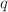$q$-geometric relations for the partition function 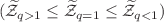$({\tilde{\mathcal{Z}}}_{q>1}\le {\tilde{\mathcal{Z}}}_{q=1}\le {\tilde{\mathcal{Z}}}_{q<1})$ and for the average energy 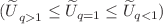${(\tilde{U}}_{q>1}\le {\tilde{U}}_{q=1}\le {\tilde{U}}_{q<1})$ can satisfy. But, we also find that the log-normal distribution and 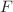$F$-distribution cannot satisfy the 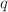$q$-geometric relation. This address can be a geometric address to choose statistics and shows the robustness of Tsallis statistics. Our results can be beneficial in assembling the next generation of quantum gates that we call polymer quantum gates.