https://doi.org/10.1140/epjp/s13360-022-02632-8
Regular Article
Relativistic thermostatistical analysis for a combined potential within spatially dependent mass scheme
1
Division of Physics Education, Hacettepe University, 06800, Ankara, Turkey
2
Department of Physics, Jahrom University, 74135-111, Jahrom, Iran
3
Department of Physics, Middle East Technical University, 06800, Ankara, Turkey
Received:
2
May
2021
Accepted:
19
March
2022
Published online:
11
April
2022
We study some thermodynamical quantities solving the Klein–Gordon equation by using a potential combining Coulomb, and Woods-Saxon potentials for a particular spatially dependent mass form. We find the energy eigenvalues, and the corresponding wave functions approximately by reforming the Klein–Gordon equation similar to a Riemann-type equation whose solutions are given in terms of hypergeometric function 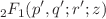 . After obtaining them analytically, we get the partition function which is based on studying the thermostatistical quantities such as specific heat and Tsallis entropy. As a function of temperature, the specific heat shows a maximum structure which is the well-known Schottky anomaly at very low temperature. Tsallis entropy enhances with increasing the temperature for different surface thickness and width of the potential.
. After obtaining them analytically, we get the partition function which is based on studying the thermostatistical quantities such as specific heat and Tsallis entropy. As a function of temperature, the specific heat shows a maximum structure which is the well-known Schottky anomaly at very low temperature. Tsallis entropy enhances with increasing the temperature for different surface thickness and width of the potential.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2022




