https://doi.org/10.1140/epjp/s13360-022-02627-5
Regular Article
Quantum-information theory of a Dirichlet ring with Aharonov–Bohm field
Department of Applied Physics and Astronomy, University of Sharjah, P.O. Box 27272, Sharjah, United Arab Emirates
Received:
8
February
2022
Accepted:
20
March
2022
Published online:
11
April
2022
Shannon quantum-information entropies 
, Fisher informations 
, Onicescu energies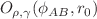 
and Rényi entropies 
are calculated both in the position (subscript 
) and momentum (
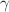) spaces as functions of the inner radius 
for the two-dimensional Dirichlet unit-width annulus threaded by the Aharonov–Bohm (AB) flux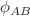 
. Small (huge) values of correspond to the thick (thin) rings with extreme of 
describing the dot. Discussion is based on the analysis of the corresponding position 
and momentum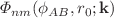 
waveforms, with n and m being principal and magnetic quantum indices, respectively: the former allows an analytic expression at any AB field whereas for the latter it is true at the flux-free configuration, 
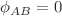, only. It is shown, in particular, that the position Shannon entropy 
[Onicescu energy 
] grows logarithmically [decreases as 
] with large tending to the same asymptote 
[
] for all orbitals whereas their Fisher counterpart 
) approaches in the same regime the m-independent limit mimicking in this way the energy spectrum variation with , which for the thin structures exhibits quadratic dependence on the principal index. Frequency of the fading oscillations of the radial parts of the wave vector functions 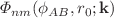increases with the inner radius what results in the identical 
asymptote for all momentum Shannon entropies 
with the alike n and different m. The same limit causes the Fisher momentum components 
to grow exponentially with . Based on these calculations, properties of the complexities 
are addressed too. Among many findings on the Rényi entropy, it is proved that the lower limit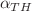 
of the semi-infinite range of the dimensionless coefficient 
, where the momentum component of this one-parameter entropy exists, is not influenced by the radius; in particular, the change of the topology from the simply, , to the doubly,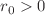 
, connected domain is unable to change 
. AB field influence on the measures is calculated too. Parallels are drawn to the geometry with volcano-shape confining potential and similarities and differences between them are discussed.
Research was supported by Competitive Research Project No. 2002143087 from the Research Funding Department, Vice Chancellor for Research and Graduate Studies, University of Sharjah.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2022
