https://doi.org/10.1140/epjp/s13360-021-01366-3
Regular Article
Quantum information measures of the Dirichlet and Neumann hyperspherical dots
Department of Applied Physics and Astronomy, University of Sharjah, P.O. Box 27272, Sharjah, United Arab Emirates
Received:
29
December
2020
Accepted:
27
March
2021
Published online:
12
April
2021
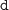-dimensional hyperspherical quantum dot with either Dirichlet or Neumann boundary conditions (BCs) allows analytic solution of the Schrödinger equation in position space and the Fourier transform of the corresponding wave function leads to the analytic form of its momentum counterpart too. This paves the way to an efficient computation in either space of Shannon, Rényi and Tsallis entropies, Onicescu energies and Fisher informations; for example, for the latter measure, some particular orbitals exhibit simple expressions in either space at any BC type. A comparative study of the influence of the edge requirement on the quantum information measures proves that the lower threshold of the semi-infinite range of the dimensionless Rényi/Tsallis coefficient where one-parameter momentum entropies exist is equal to 
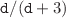for the Dirichlet hyperball and 
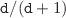for the Neumann one what means that at the unrestricted growth of the dimensionality both measures have their Shannon fellow as the lower verge. Simultaneously, this imposes the restriction on the upper value of the interval 
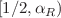inside which the Rényi uncertainty relation for the sum of the position 
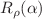and wave vector 
components is defined: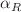 
is equal to 
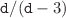for the Dirichlet geometry and to 
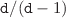for the Neumann BC. Some other properties are discussed from mathematical and physical points of view. Parallels are drawn to the corresponding properties of the hydrogen atom and similarities and differences are explained based on the analysis of the associated wave functions.
Research was supported by Competitive Research Project No. 2002143087 from the Research Funding Department, Vice Chancellor for Research and Graduate Studies, University of Sharjah.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2021
