Eur. Phys. J. Plus (2021) 136: 249
https://doi.org/10.1140/epjp/s13360-021-01250-0

Regular Article

Isochronous n-dimensional nonlinear PDM-oscillators: linearizability, invariance and exact solvability

Department of Physics, Eastern Mediterranean University, G. Magusa, North Cyprus, Mersin 10, Turkey

^a omar.mustafa@emu.edu.tr

Received: 7 December 2020
Accepted: 17 February 2021
Published online: 22 February 2021

Abstract

Within the standard Lagrangian settings (i.e., the difference between kinetic and potential energies), we discuss and report isochronicity, linearizability and exact solubility of some n-dimensional nonlinear position-dependent mass (PDM) oscillators. In the process, negative the gradient of the PDM potential force field is shown to be no longer related to the time derivative of the canonical momentum, 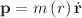$\mathbf{p}=m\left(r\right)\dot{\mathbf{r}}$, but it is rather related to the time derivative of the pseudo-momentum, 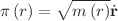$\mathit{\pi }\left(r\right)=\sqrt{m\left(r\right)}\dot{\mathbf{r}}$ (i.e., Noether momentum). Moreover, using some point transformation recipe, we show that the linearizability of the n-dimensional nonlinear PDM-oscillators is only possible for 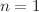$n=1$ but not for $n\ge 2$. The Euler–Lagrange invariance falls short/incomplete for $n\ge 2$ under PDM settings. Alternative invariances are sought, therefore. Such invariances, like Newtonian invariance of Mustafa (Phys Scr 95:065214, 2020), effectively authorize the use of the exact solutions of one system to find the solutions of the other. A sample of isochronous n-dimensional nonlinear PDM-oscillators examples is reported.