Position-dependent mass momentum operator and minimal coupling: point canonical transformation and isospectrality

Omar Mustafa; Zeinab Algadhi

doi:10.1140/epjp/i2019-12588-y

EPJ

a
b
c
d
e
ap
st
h
plus
ds
pv
ti
qt
am
n

2024 Impact factor 2.9

EPJ PLUS - Condensed Matter and Complex Systems

Eur. Phys. J. Plus (2019) 134: 228
https://doi.org/10.1140/epjp/i2019-12588-y

Regular Article

Position-dependent mass momentum operator and minimal coupling: point canonical transformation and isospectrality

Omar Mustafa^* and Zeinab Algadhi

Department of Physics, Eastern Mediterranean University, G. Magusa, 10, Mersin, North Cyprus, Turkey

^* e-mail: omar.mustafa@emu.edu.tr

Received: 1 November 2018
Accepted: 18 February 2019
Published online: 27 May 2019

Abstract

The classical and quantum-mechanical correspondence for constant mass settings is used, along with some point canonical transformation, to find the position-dependent mass (PDM) classical and quantum Hamiltonians. The comparison between the resulting quantum PDM-Hamiltonian and the von Roos PDM-Hamiltonian implied that the ordering ambiguity parameters of von Roos are strictly determined. Eliminating, in effect, the ordering ambiguity associated with the von Roos PDM-Hamiltonian. This, consequently, played a vital role in the construction and identification of the PDM-momentum operator. The same recipe is followed to identify the form of the minimal coupling of electromagnetic interactions for the classical and quantum PDM-Hamiltonians. 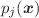It turned out that whilst the minimal coupling may very well inherit the usual form in classical mechanics (i.e., $p_{j} (\vec{x}) \rightarrow p_{j}(\vec{x}) -e A_{j}(\vec{x})$ , where $p_{j}(\vec{x})$ is the j-th component of the classical PDM-canonical-momentum), it admits a necessarily different and vital form in quantum mechanics (i.e., $\hat{p}_{j}(\vec{x})/\sqrt{m(\vec{x})} \rightarrow (\hat{p}_{j}(\vec{x})$ $-e A_{j}(\vec{x}))/\sqrt{m(\vec{x})}$ , where $\hat{p}_{j}(\vec{x})$ is the j-th component of the quantum PDM-momentum operator). Under our point transformation settings, only one of the two commonly used vector potentials (i.e., $\vec{A} (\vec{x}) \sim (-x_{2}, x_{1}, 0)$ ) is found eligible and is considered for our Illustrative examples.