Eur. Phys. J. Plus (2020) 135: 559
https://doi.org/10.1140/epjp/s13360-020-00529-y

Regular Article

Position-dependent mass charged particles in magnetic and Aharonov–Bohm flux fields: separability, exact and conditionally exact solvability

Department of Physics, Eastern Mediterranean University, G. Magusa, North Cyprus, Mersin 10, Turkey

^a omar.mustafa@emu.edu.tr

Received: 8 October 2019
Accepted: 11 June 2020
Published online: 10 July 2020

Abstract

Using cylindrical coordinates, we consider position-dependent mass (PDM) charged particles moving under the influence of magnetic, Aharonov–Bohm flux, and a pseudoharmonic or a generalized Killingbeck-type potential fields. We implement the PDM minimal coupling recipe (Mustafa in J Phys A Math Theor 52:148001, 2019), along with the PDM-momentum operator (Mustafa and Algadhi in Eur Phys J Plus 134:228, 2019), and report separability under radial cylindrical and azimuthal symmetrization settings. 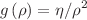For the radial Schrödinger part, we transform it into a radial one-dimensional Schrödinger-type and use two PDM settings, $g\left(\rho \right)=\eta {\rho }^2$ and $g\left(\rho \right)=\eta /{\rho }^2$, to report on the exact solvability of PDM charged particles moving in three fields: magnetic, Aharonov–Bohm flux, and pseudoharmonic potential fields. 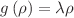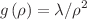Next, we consider the radial Schrödinger part as is and use the biconfluent Heun differential forms for two PDM settings, $g\left(\rho \right)=\lambda \rho$ and $g\left(\rho \right)=\lambda /{\rho }^2$, to report on the conditionally exact solvability of our PDM charged particles moving in three fields: magnetic, Aharonov–Bohm flux, and generalized Killingbeck potential fields. Yet, we report the spectral signatures of the one-dimensional z-dependent Schrödinger part on the overall eigenvalues and eigenfunctions, for all examples, using two z-dependent potential models (infinite potential well and Morse-type potentials).