https://doi.org/10.1140/epjp/s13360-020-00979-4
Regular Article
A mathematical and parametric study of epidemiological smoking model: a deterministic stability and optimality for solutions
1
Department of Mathematics, COMSATS University Islamabad, Attock Campus, Attock, Pakistan
2
Department of Mathematics, University of the Punjab, 54590, Lahore, Pakistan
3
Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
4
Institute of Ground Water Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, Bloemfontein, South Africa
5
Department of Basic Sciences and Related Studies, Mehran University of Engineering and Technology, Jamshoro, Pakistan
c
kashif.abro@faculty.muet.edu.pk
Received:
2
November
2020
Accepted:
30
November
2020
Published online:
2
January
2021
The qualitative study of a smoking model with parametric conditions for diseases controlling under the influence of smoking is investigated through rigorous mathematical study. The mathematical modeling of epidemiological smoking model having six compartments is traced out. Mathematical expressions for smoke-free and smoke-present equilibrium points have been developed. The strength of Lyapunov functional theory has been exploited to show that smoke-free equilibrium point is globally asymptotically stable whenever basic reproduction number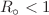 
. The competency of graphical and theoretic process is utilized to observe the global behavior of unique smoke equilibrium point. The sensitivity analysis of the model is performed through the basic reproduction number and diseased classes effectively to design reliable, robust and stable control strategies.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2021
