Fractional Hunter-Saxton equation involving partial operators with bi-order in Riemann-Liouville and Liouville-Caputo sense

J. F. Gómez-Aguilar; Abdon Atangana

doi:10.1140/epjp/i2017-11371-6

EPJ

Fractional Hunter-Saxton equation involving partial operators with bi-order in Riemann-Liouville and Liouville-Caputo sense

J. F. Gómez-Aguilar¹^* and Abdon Atangana²

¹ CONACyT-Centro Nacional de Investigación y Desarrollo Tecnológico, Tecnológico Nacional de México, Interior Internado Palmira S/N, Col. Palmira, Cuernavaca, C.P. 62490, Morelos, Mexico
² Institute for Groundwater Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, 9300, Bloemfontein, South Africa

Received: 18 December 2016
Accepted: 24 January 2017
Published online: 28 February 2017

Abstract

In this work the fractional Hunter-Saxton equation applied in the study of diffusion of nematic liquid crystals was done involving partial operators with two fractional orders, 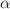$\alpha$ and $\beta$ , via Atangana-Riemann and Atangana-Caputo with bi-order and via Riemann-Liouville, Caputo-Fabrizio-Riemann and Atangana-Baleanu-Riemann for the space domain. The mathematical equation underpinning this physical phenomenon was solved numerically using an iterative scheme where the numerical approximations for second order were developed. The new approach with two fractional orders is able to consider media with two different layers, scales and properties. The generalization of this equation exhibit different cases of anomalous behavior and the numerical solutions obtained describes the propagation of waves in a nematic liquid cristal.

15th European Conference on Atoms Molecules and Photons (ECAMP)
June 30 to July 4, 2025
Innsbruck, Austria

EPJ

Fractional Hunter-Saxton equation involving partial operators with bi-order in Riemann-Liouville and Liouville-Caputo sense

Conference announcements