Eur. Phys. J. Plus (2016) 131: 335
https://doi.org/10.1140/epjp/i2016-16335-8

Regular Article

Numerical solution of fractional-in-space nonlinear Schrödinger equation with the Riesz fractional derivative

Institute for Groundwater Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, 9300, Bloemfontein, South Africa

^* e-mail: mkowolax@yahoo.com

Received: 9 August 2016
Accepted: 24 August 2016
Published online: 26 September 2016

Abstract

In this paper, dynamics of time-dependent fractional-in-space nonlinear Schrödinger equation with harmonic potential 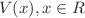in one, two and three dimensions have been considered. We approximate the Riesz fractional derivative with the Fourier pseudo-spectral method and advance the resulting equation in time with both Strang splitting and exponential time-differencing methods. The Riesz derivative introduced in this paper is found to be so convenient to be applied in models that are connected with applied science, physics, and engineering. We must also report that the Riesz derivative introduced in this work will serve as a complementary operator to the commonly used Caputo or Riemann-Liouville derivatives in the higher-dimensional case. In the numerical experiments, one expects the travelling wave to evolve from such an initial function on an infinite computational domain 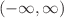, which we truncate at some large, but finite values L. It is important that the value of L is chosen large enough to give enough room for the wave function to propagate. We observe a different distribution of complex wave functions for the focusing and defocusing cases.