Eur. Phys. J. Plus (2014) 129: 170
https://doi.org/10.1140/epjp/i2014-14170-7

Regular Article

Natural convection on a vertical plate in a saturated porous medium with internal heat generation

¹ University of Picardie Jules-Verne, Faculty of Mathematics and Computer Science, 33, Rue Saint-Leu, 80039, Amiens, France
² University of Sidi Mohamed Ben Abdellah, Polydisciplinary Faculty of Taza, BP.1223, LIMAO, Taza, Morocco

^* e-mail: driss_achemlal@yahoo.fr

Received: 20 March 2014
Revised: 16 July 2014
Accepted: 17 July 2014
Published online: 15 August 2014

Abstract

The main goal of this paper is to re-exam a class of exact solutions for the two-dimensional free convection boundary layers induced by a heated vertical plate embedded in a saturated porous medium with an exponential decaying heat generation. The temperature distribution of the plate has been assumed to vary as a power of the axial coordinate measured from the leading edge of the plate and subjected to an applied lateral mass flux. The boundary layer equations are solved analytically and numerically using a fifth-order Runge-Kutta scheme coupled with the shooting iteration method. As for the classical problem without internal heat generation, it is proved that multiple (unbounded) solutions arise for any 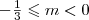and for any suction/injection parameter. For such solutions, the asymptotic behavior as the similarity variable approaches infinity is determined.