https://doi.org/10.1140/epjp/i2014-14169-0
Regular Article
Construction of basis vectors for symmetric irreducible representations of O(5) 
O(3)
1
Department of Physics, Liaoning Normal University, 116029, Dalian, China
2
Department of Physics and Astronomy, Louisiana State University, 70803-4001, Baton Rouge, LA, USA
3
School of Mathematics and Physics, The University of Queensland, Qld 4072, Brisbane, Australia
* e-mail: daipan@dlut.edu.cn
Received:
14
April
2014
Revised:
30
June
2014
Accepted:
9
July
2014
Published online:
13
August
2014
A recursive method for the construction of symmetric irreducible representations of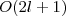 
in the 
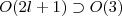basis for identical boson systems is proposed. The formalism is realized based on the group chain 
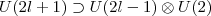, of which the symmetric irreducible representations are simply reducible. The basis vectors for symmetric irreducible representations of the 
can easily be constructed from those of U(2l + 1)
U(2l - 1) ⊗ U(2)
O(2l - 1) ⊗ U(1) with no l -boson pairs, namely with the total boson number exactly equal to the seniority number in the system, from which one can construct symmetric irreducible representations of 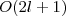in the 
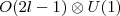basis when all symmetric irreducible representations of O(2l - 1) are known. As a starting point, basis vectors of symmetric irreducible representations of O(5) are constructed in the 
basis, where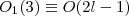 
, when l = 2 , which is generated not by the angular momentum operators of the d -boson system, but by the operators constructed from d -boson creation (annihilation) operators 
( 
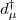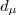with 
, 0, -1 . Matrix representations of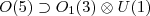 
, together with the elementary Wigner coefficients, are presented. After the angular momentum projection, a three-term relation in determining the expansion coefficients of the 
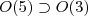basis vectors, where the O(3) group is generated by the angular momentum operators of the d -boson system, in terms of those of is derived. The eigenvectors of the projection matrix with zero eigenvalues constructed according to the three-term relation completely determine the basis vectors of 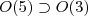. Formulae for evaluating the elementary Wigner coefficients of 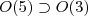are derived explicitly. Analytical expressions of some elementary Wigner coefficients of 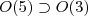for the coupling 
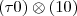with resultant angular momentum quantum number L = 2
+ 2 - k for 
with a multiplicity 2 case for k = 6 are presented.
© Società Italiana di Fisica and Springer-Verlag Berlin Heidelberg, 2014
