https://doi.org/10.1140/epjp/s13360-025-06640-2
Regular Article
Hartmann potential and phase space perspective
1
PTEA Laboratory, Physics Department, Faculty of Sciences, Yahia FARES University, 26000, Médéa, Algeria
2
LPTHIRM, Département de Physique, Faculté des Sciences, Université Saâd DAHLAB-Blida 1, B.P. 270 Route de Soumâa, 09000, Blida, Algeria
a
cherroud.othmane@univ-medea.dz
Received:
1
May
2025
Accepted:
8
July
2025
Published online:
30
July
2025
This contribution represents a formulation of quantum mechanics in phase space, aimed at the simultaneous construction of the non-central Hartmann (ring-shaped) potential within two approaches, which are Wigner’s distribution function and the characteristic function. Through Weyl’s transforms, two independent computational methods were developed, each leading to the same general expression for higher-order moments of position and momentum, thereby ensuring the robustness of the mathematical formulation. A general analytical expression for the momentum operator was also derived, offering a novel and complementary contribution to the study of the non-central Hartmann potential. Furthermore, we establish an analytical form of Heisenberg’s uncertainty principle, explicitly dependent on the quantum number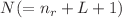 
and angular quantum number L. The consistency of the Heisenberg–Born–Jordan–Dirac commutation relation has also been verified within this framework.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
