https://doi.org/10.1140/epjp/s13360-025-06483-x
Regular Article
Perfect state transfer on several types of graphs based on the quantum probability perspective
College of Mathematics and Statistics, Northwest Normal University, 730070, Lanzhou, China
Received:
6
January
2025
Accepted:
27
May
2025
Published online:
17
June
2025
The transfer of quantum states plays an important role in quantum information. The fidelity of quantum states transferred from one vertex to another has always been the focus of attention. In this paper, we study the perfect state transfer on several graphs, namely the complete bipartite graph 
, the two-dimensional hypercube, the three-dimensional hypercube, the 
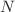-fold star power 
and the finite path graph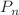 
. We obtain the Hamiltonian of the graphs by designing the coupling strength between antipodes vertices and using mirror symmetry. Since the several types of graphs we selected are highly symmetrical, based on the idea of quantum probability, we adopt the method of spectral distribution of the adjacency matrix to divide the graphs into the union of disjoint strata, making the fixed origin on the graph to achieve perfect state transfer with the vertices of each stratum. In particular, we find that the 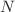-fold star power has perfect state transfer only when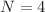 
under this method. In addition, for the finite path graph 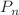, we obtain conclusions that are consistent with the known results.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
