https://doi.org/10.1140/epjp/s13360-025-06289-x
Regular Article
On the exact traveling wave solutions to the Akbota-Gudekli-Kairat-Zhaidary equation and its numerical solutions
1
Department of Basic Science, Faculty of Engineering, Benha University, Shubra, Egypt
2
Neighborhood of Akcaglan, Imarli Street, Number: 28/4, 26030, Eskisehir, Turkey
Received:
30
October
2024
Accepted:
2
April
2025
Published online:
3
May
2025
In this work, we will study one of the notable integrable models, the Akbota-Gudekli-Kairat-Zhaidary Equation, which belongs to a class of integrable space curves and surfaces. It exhibits a wide range of traveling wave solutions, facilitated by the existence of a Lax pair associated with the nonlinear differential equation. The primary focus of this article is the extraction of the exact traveling wave solutions of this model for the first time, employing two distinct semi-analytical techniques, namely the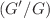 
-expansion method and the Paul-Painlevé approach method. Throughout these two suggested universal techniques, various types of exact traveling wave solutions such as W-like soliton solution, M-like soliton solution, Bright soliton solution, Dark soliton solution, hyperbolic function soliton solution and other rational soliton solutions have been attained. Besides the two semi-analytic methods, the well-known simple and efficient numerical method called the differential transform method is taking into account to introduce the numerical approximation corresponding to the semi-analytical solutions obtained previously. To illustrate the consistent between the exact traveling wave solutions and numerical solutions we demonstrate the plot the 2D and 3D graphs that explore the dynamical behaviors of the extracted exact traveling wave solutions. The realized solutions show the dynamic properties of the soliton arising from the suggested model and will help to introduce future studies for all related phenomena.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
