Eur. Phys. J. Plus (2024) 139: 923
https://doi.org/10.1140/epjp/s13360-024-05700-3

Regular Article

Coherent states of an accelerated particle

¹ Department of Physics, Tomsk State University, Lenin ave. 36, 634050, Tomsk, Russia
² P.N. Lebedev Physical Institute, Leninskiy ave. 53, 119991, Moscow, Russia
³ Institute of Physics, University of São Paulo, Rua do Matão, 1371, 05508-090, São Paulo, Brazil

^a breev@mail.tsu.ru

Received: 1 July 2024
Accepted: 26 September 2024
Published online: 23 October 2024

Abstract

We construct generalized coherent states (GCS) of a massive accelerated particle. This example is an important step in studying coherent states (CS) for systems with an unbounded motion and a continuous spectrum. First, we represent quantum states of the accelerated particle both known and new ones obtained by us using the method of non-commutative integration of linear differential equations. A complete set of non-stationary states for the accelerated particle is obtained. This set is expressed via elementary functions and is characterized by a continuous real parameter 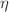$\eta$, which corresponds to the initial momentum of the particle. A connection is obtained between these solutions and stationary states, which are determined by the Airy function. We solved the problem of constructing GCS, in particular, semiclassical states describing the accelerated particle, within the framework of the consistent method of integrals of motion. We have found different representations, coordinate one and in a Fock space, analyzing in detail all the parameters entering in these representations. We prove corresponding completeness and orthogonality relations. Conditions for minimizing uncertainty relations were studied, and the set of the corresponding parameters was determined. From the GCS, a family of states is isolated, which usually is called the CS. This family of states is parameterized by a real parameter 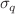${\sigma }_q$, which has the meaning of the standard deviation of the coordinate at the initial time instant. The CS minimize the Robertson–Schrödinger uncertainty relation at all the time instants and the Heisenberg uncertainty relation at the initial time. The probability density is given by a Gaussian distribution with the standard deviations ${\sigma }_q(\tau )$ at the time $\tau$. Coordinate mean values are moving along classical trajectories of the accelerated particles and coincide with trajectories of the maximum of the wave packets. We prove the completeness and orthogonality relations for the obtained GCS and CS. Standard deviations for the GCS and CS are calculated. On this base, and considering the change in the shape of wave packets with time, we define general conditions of the semi-classicality and a class of the CS that can be identified with semiclassical states. As follows from these conditions, in contrast to a free particle case, where CS can be considered as semiclassical states if the Compton wavelength of the particle is much less than the coordinate standard deviation at the initial time moment, after a sufficiently long time period, the CS of the accelerated particle can be always considered as semiclassical ones. It is interesting that this conclusion is matched with the one obtained in a recent work by Sazonov, in studying the Caldirola–Kanai model. Namely, there were demonstrated that the force of resistance and viscous friction prevent the spreading of a quasi-classical wave packet. Thus, the resistance force suppresses the quantum properties of the particle, increasingly highlighting the classical features in its movement over the time.