https://doi.org/10.1140/epjp/s13360-024-05617-x
Regular Article
A simple model of magnetic universe without singularity associated with a quadratic equation of state
Laboratoire de Physique Théorique, CNRS, UPS, Université de Toulouse, Toulouse, France
Received:
31
May
2024
Accepted:
2
September
2024
Published online:
10
October
2024
A model of magnetic universe based on nonlinear electrodynamics has been introduced by Kruglov (Phys Rev D 92:123523, 2015). This model describes an early inflation era followed by a radiation era. We show that this model is related to the model of universe based on a quadratic equation of state introduced in our previous paper (Chavanis in Universe 1:357, 2015). This correspondence may provide a more fundamental justification of our equation of state. It may arise from quantum corrections to linear electrodynamics when the electromagnetic field becomes very high. We discuss two quantitatively different models of early universe. In Model I, the primordial density of the universe is identified with the Planck density. At 
, the universe had the characteristics of a Planck black hole (“planckion” particle). During the inflation, which takes place on a Planck timescale, the size of the universe evolves from the Planck length to a size comparable to the Compton wavelength of the neutrino. If we interpret the radius of the universe at the end of the inflation (neutrino’s Compton wavelength) as a minimum length related to quantum gravity and use Zeldovich’s first formula of the vacuum energy, we obtain the correct value of the cosmological constant. In Model II, the primordial density of the universe is identified with the electron density as a consequence of nonlinear electrodynamics. At , the universe had the characteristics of an electron. This can be viewed as a refinement of the “primeval atom” of Lemaître. During the inflation, which takes place on a gravitoelectronic timescale, the size of the universe evolves from the electron’s classical radius to a size comparable to the size of a dark energy star of the stellar mass. If we interpret the radius of the universe at the beginning of the inflation (electron’s classical radius) as a minimum length related to quantum gravity and use Zeldovich’s second formula of the vacuum energy, we obtain the correct value of the cosmological constant. This provides an accurate form of Eddington’s relation between the cosmological constant and the mass of the electron. We use these arguments to show that the present universe contains about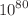 
protons (Eddington’s number). We also introduce a nonlinear electromagnetic Lagrangian that describes simultaneously the early inflation, the radiation era, and the dark energy era. It may account for a form of “generalized radiation” that is present from the beginning to the end of the cosmic evolution. Baryonic and dark matter are treated as independent noninteracting species. The dark energy era is due to the electromagnetic vacuum energy (zero-point radiation). In this approach, both the early inflation and the late acceleration of the universe (dark energy) arise as a consequence of nonlinear electrodynamics. This leads to a simple model of magnetic universe without singularity (aioniotic universe).
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
