https://doi.org/10.1140/epjp/s13360-024-05501-8
Regular Article
New procedure for evaluation of U(3) coupling and recoupling coefficients
1
Department of Physics and Astronomy, Louisiana State University, 70803-4001, Baton Rouge, LA, USA
2
Department of Physics, Liaoning Normal University, 116029, Dalian, China
Received:
13
May
2024
Accepted:
26
July
2024
Published online:
8
August
2024
A simple method to calculate Wigner coupling coefficients and Racah recoupling coefficients for U(3) in two group–subgroup chains is presented. While the canonical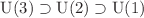 
coupling and recoupling coefficients are applicable to any system that respects U(3) symmetry, the 
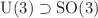coupling coefficients are more specific to nuclear structure studies. This new procedure precludes the use of binomial coefficients and alternating sums which were used in the 1973 formulation of Draayer and Akiyama, and in so doing provides a faster and more accurate determination of any and all required results. The resolution of the outer multiplicity is based on the null space concept of the U(3) generators proposed by Alex et al., whereas the inner multiplicity in the angular momentum subgroup chain is obtained from the dimension of the null space of the SO(3) raising operator. It is anticipated that a C++ library will ultimately be available for determining generic coupling and recoupling coefficients associated with both the canonical and the physical group–subgroup chains of U(3).
© The Author(s) 2024
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
