Explanation of the generalizations of uncertainty principle from coordinate and momentum space periodicity

Subir Ghosh

doi:10.1140/epjp/s13360-024-05366-x

2024 Impact factor 2.9

EPJ PLUS - Condensed Matter and Complex Systems

Eur. Phys. J. Plus (2024) 139: 569
https://doi.org/10.1140/epjp/s13360-024-05366-x

Regular Article

Explanation of the generalizations of uncertainty principle from coordinate and momentum space periodicity

Subir Ghosh^a

Physics and Applied Mathematics Unit, Indian Statistical Institute, 203 B. T. Road, 700108, Kolkata, India

^a subirghosh20@gmail.com

Received: 18 April 2024
Accepted: 15 June 2024
Published online: 2 July 2024

Abstract

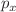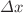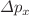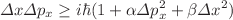Generalizations of coordinate x-momentum $p_{x}$ $$p_x$$ uncertainty principle, with $Δ x$ $\Delta x$ - and $Δ p_{x}$ $\Delta p_x$ -dependent terms ( $Δ$ $\Delta$ denoting standard deviation), $\begin{matrix} Δ x Δ p_{x} \geq i ħ (1 + α Δ p_{x}^{2} + β Δ x^{2}) \end{matrix}$ $\begin{aligned} \Delta x \Delta p_x\ge i\hbar (1+\alpha \Delta p_x^2 +\beta \Delta x^2) \end{aligned}$ have provided rich dividends as a poor person’s approach toward quantum gravity, because these can introduce coordinate and momentum scales ( 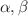$α, β$ $\alpha ,\beta$ ) that are appealing conceptually. However, these extensions of uncertainty principle are purely phenomenological in nature. Apart from the inherent ambiguity in their explicit structures, the introduction of generalized commutations relations compatible with the uncertainty relations has some drawbacks. In the present paper, we reveal that these generalized uncertainty principles can appear in a perfectly natural way, in canonical quantum mechanics, if one assumes a periodic nature in coordinate or momentum space, as the case may be. We bring in to light quite old (but not so well known) works by Judge and by Judge and Lewis that explain in detail how a consistent and generalized uncertainty principle is induced in the case of angle 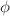$ϕ$ $\phi$ —angular momentum $L_{z}$ $$L_z$$ , $\begin{matrix} Δ ϕ Δ L_{z} \geq i ħ (1 + ν Δ ϕ^{2}) \end{matrix}$ $\begin{aligned} \Delta \phi \Delta L_z \ge i\hbar (1 +\nu \Delta \phi ^2) \end{aligned}$ purely from a consistent implementation of periodic nature of the angle variable $ϕ$ $\phi$ , 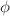without changing the 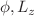$ϕ, L_{z}$ $\phi , L_z$ canonical commutation relation. Structurally this is identical to the well-known extended uncertainty principle. We directly apply this formalism to formulate the 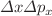$Δ x Δ p_{x}$ $\Delta x \Delta p_x$ extended uncertainty principle. We identify 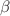$β$ $\beta$ with an observed length scale relevant in astrophysics context. We speculate about the 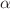$α$ $\alpha$ extension.

Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Conference announcements

12 Internat. Congress of the Balkan Physical Union
July 8-12, 2025
Bucharest, Romania

Joint Annual Meeting of ÖPG and SPS
August 18-22, 2025
Wien, Austria

111th Italian National Society Congress
September 22-26, 2025
Palermo, Italy

EPJ

Explanation of the generalizations of uncertainty principle from coordinate and momentum space periodicity

Conference announcements