https://doi.org/10.1140/epjp/s13360-024-05086-2
Regular Article
An exact solution for the magnetic diffusion problem with a step-function resistivity model
1
Institute of Fluid Physics, China Academy of Engineering Physics, 621999, Mianyang, People’s Republic of China
2
Hunan Shaofeng Institute for Applied Mathematics, National Center for Applied Mathematics in Hunan, 411105, Xiangtan, People’s Republic of China
3
Hunan Key Laboratory for Computation and Simulation in Science and Engineering, Xiangtan University, 411105, Xiangtan, People’s Republic of China
4
School of Mathematics and Computational Science, Xiangtan University, 411105, Xiangtan, People’s Republic of China
Received:
25
December
2023
Accepted:
10
March
2024
Published online:
2
April
2024
In the magnetic diffusion problem, a magnetic diffusion equation is coupled by an Ohmic heating energy equation. The Ohmic heating can make the magnetic diffusion coefficient (i.e. the resistivity) vary violently, and make the diffusion a highly nonlinear process. For this reason, the problem is normally very hard to be solved analytically. In this article, under the condition of a step-function resistivity and a constant boundary magnetic field, we successfully derived an exact solution for this nonlinear problem. The solution takes four parameters as input: the fixed magnetic boundary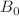 
, 
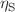and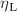 
that are resistivities below and above the critical energy density of a material, and the critical energy density 
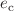of the material. The solution curve B(x, t) possesses the characteristic of a sharp front, and its evolution obeys the usual self-similar rule with the similarity variable 
.
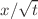Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
