https://doi.org/10.1140/epjp/s13360-023-04736-1
Regular Article
Physical phenomena analysis of solution structures in a nonlinear electric transmission network with dissipative elements
1 Mechanical College, Shanghai Dianji University, Shanghai, People’s Republic of China
2 School of Business, Shanghai Dianji University, Shanghai, People’s Republic of China
Received:
4
September
2023
Accepted:
23
November
2023
Published online: 2 January 2024
We utilize a novel approach to seek exact solutions for the multi-coupled discrete nonlinear transmission electrical network. With the assistance of MATLAB R2021a software, the paper presents six key aspects that contribute to its novelty: (1) In this study, we introduce the (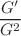
)-expansion method to explore the exact solutions of the voltage equation in a multi-coupled discrete nonlinear transmission electric network (Fig. 1 in Sect. 1). (2) This paper inaugural explores the application of fractional-order derivatives in studying the characteristics of Fig. 1. Fractional-order derivatives are utilized due to their ability to capture the memory effect, providing a more accurate characterization of current and voltage. (3) We first investigate the influence of fractions on signal transmission, specifically focusing on their effects on signal voltage width, amplitude, and propagation direction. (4) Building upon the works of Kengne et al. (Phys Rep 982:1–124, 2022), Kengne (Chaos Soliton Fractals 146:110866, 2021), Kengne (Chaos Soliton Fractals 164:112637, 2022), Djelah et al. (Chaos Soliton Fractals 167:113087, 2023), we conducted a first investigation into the impact of the dispersion element Cs on transmission voltage. Our study unveiled that Cs induces variations in voltage amplitude and provides compensation for the transmission signal, thereby playing a vital role in ensuring stability and reliability. (5) This study pioneers the investigation of the exact solution changes in the voltage equation for the nonlinear transmission electric network by varying obliqueness angles 
. (6) This study presents a novel comparison of the effects of multiple fractional derivatives on the voltage generated by the nonlinear transmission electric network. Our findings reveal that the disparities among different fractional derivative orders are insignificant. We employ graphical simulations to investigate the impact of varying parameters in the aforementioned (1)-(6) on the voltage waveform. Our analysis reveals that the propagation of voltage waves is influenced by factors such as the fractional order, wave obliqueness angles, and other pertinent physical parameters. These aspects have not been addressed in the previous works of Kengne et al. (Phys Rep 982:1–124, 2022), Kengne (Chaos Soliton Fractals 146:110866, 2021), Kengne et al. (Phys Rev E 74(3):036614, 2006), Kengne (Chaos Soliton Fractals 164:112637, 2022).
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
