https://doi.org/10.1140/epjp/s13360-023-04402-6
Regular Article
A conservative splitting high-order finite difference method for coupled Gross–Pitaevskii equations in 2D
Department of Mathematical Sciences, University of Puerto Rico, Call Box 9000, 00681, Mayagüez, PR, USA
Received:
29
October
2022
Accepted:
21
August
2023
Published online:
5
September
2023
An energy conservative field directional scheme to approximate the solution of Gross–Pitaevskii systems of nonlinear equations in 2D is derived from the general idea of the Lie–Trotter splitting technique. In addition, the method preserves a numerical invariant which can be interpreted as a time step perturbation of the total mass. Under certain conditions, e.g., when the Josephson junction is neglected or when the initial conditions satisfy certain algebraic properties, mass conservation is also achieved. Using a suitable class of high-order symmetric finite difference approximations of the Laplacian operator in 2D, we prove that, for the thermodynamically stable regime, the directional splitting scheme is of order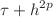 
in the 
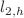-norm, for 
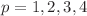. High-order accuracy in time can be achieved by combining the proposed basic time step with well-known composition methods, as a result conservative methods of order 
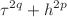with 
are obtained. Conservation and accuracy are numerically validated for model problems with and without internal atomic Josephson junction. Our performance study shows that the proposed technique is suitable for long-term simulations.
Axi Aguilera and Jason Bermudez These authors have contributed equally to this work.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
