https://doi.org/10.1140/epjp/s13360-023-04277-7
Regular Article
Global dynamic analysis of a nonlinear state-dependent feedback control SIR model with saturation incidence
1
School of Mathematics and Information Science, Zhengzhou University of Light Industry, 450002, Zhengzhou, China
2
School of Mathematics and Statistics, Huanghuai University, 463000, Zhumadian, China
Received:
10
May
2023
Accepted:
11
July
2023
Published online:
21
July
2023
This paper investigates an SIR model with nonlinear state-dependent feedback control. The saturation incidence rate is introduced into the classical SIR model, and the specific expression of the equilibrium point of the model without pulse control is derived, and the stability of the equilibrium point is analyzed. When the number of susceptible individuals reaches a threshold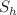 
, comprehensive prevention and control strategies such as treatment, isolation, and vaccination will be implemented. The existence and global stability of the disease-free periodic solution (DFPS) of the model with state-dependent feedback control are discussed, and the properties of the Poincaré map are analyzed. Based on the bifurcation theory related to a one-parameter family of maps associated with the Poincaré map, we define the control reproduction number 
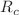based on different parameters and observe the effect of these parameters on bifurcation. Numerical simulations show that transcritical and pitchfork bifurcations, as well as backward bifurcations, may occur under certain conditions. Additionally, a sensitivity analysis of 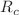is conducted, and the optimal control strategy for the SIR model without pulse control is discussed. These results can provide some suggestions for virus control and vaccine production, among other issues.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
