https://doi.org/10.1140/epjp/s13360-023-04253-1
Regular Article
Complementary dual skew polycyclic codes and their applications to EAQECCs
Department of Mathematics, Indian Institute of Technology Patna, 801 106, Patna, India
Received:
16
April
2023
Accepted:
4
July
2023
Published online:
21
July
2023
For integers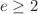 
, 
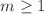and a prime p, consider the ring 
, 
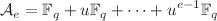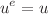where 
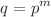and e satisfies 
. This work investigates skew polycyclic codes over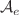 
. Using the idempotent decomposition technique, we present the generator polynomial and generator matrix of skew polycyclic codes over 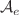. Then we determine the necessary and sufficient conditions for these codes to be self-dual and derive some conditions under which skew polycyclic codes satisfy the complementary duality property. Further, we define a Gray map and investigate the Gray image of an LCD (or self-dual) code over 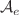. Besides, we also present a construction of LCD codes from self-dual codes (see Theorem 13). Finally, several examples of entanglement-assisted quantum error-correcting codes obtained from LCD codes are provided.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
