https://doi.org/10.1140/epjp/s13360-023-04202-y
Regular Article
Higher-order curvature operators in causal set quantum gravity
1
CP3-Origins, University of Southern Denmark, Campusvej 55, 5230, Odense M, Denmark
2
Niels Bohr Institute, University of Copenhagen, Blegdamsvej 17, 2100, Copenhagen, Denmark
Received:
1
February
2023
Accepted:
17
June
2023
Published online:
6
July
2023
We construct higher-order curvature invariants in causal set quantum gravity. The motivation for this work is twofold: First, to characterize causal sets, discrete operators that encode geometric information on the emergent spacetime manifold, e.g., its curvature invariants, are indispensable. Second, to make contact with the asymptotic-safety approach to quantum gravity in Lorentzian signature and find a second-order phase transition in the phase diagram for causal sets, going beyond the discrete analog of the Einstein–Hilbert action may be critical. Therefore, we generalize the discrete d’Alembertian, which encodes the Ricci scalar, to higher orders. We prove that curvature invariants of the form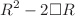 
(and similar invariants at higher powers of derivatives) arise in the continuum limit.
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1140/epjp/s13360-023-04202-y.
© The Author(s) 2023
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
