https://doi.org/10.1140/epjp/s13360-023-04014-0
Regular Article
COVID-19 multiwaves as multiphase percolation: a general N-sigmoidal equation to model the spread
1
Preparatory Institute of Engineering of Tunis. Materials and Fluids Laboratory, University of Tunis, Tunis, Tunisia
2
The Higher Institute of Sciences and Technologies of the Environnent Borj Cedria, University of Carthage, Carthage, Tunisia
Received:
13
February
2023
Accepted:
20
April
2023
Published online:
8
May
2023
The aim of the current study is to investigate the spread of the COVID-19 pandemic as a multiphase percolation process. Mathematical equations have been developed to describe the time dependence of the number of cumulative infected individuals,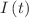 
, and the velocity of the pandemic, 
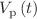, as well as to calculate epidemiological characteristics. The study focuses on the use of sigmoidal growth models to investigate multiwave COVID-19. Hill, logistic dose response and sigmoid Boltzmann models fitted successfully a pandemic wave. The sigmoid Boltzmann model and the dose response model were found to be effective in fitting the cumulative number of COVID-19 cases over time 2 waves spread (N = 2). However, for multiwave spread (N > 2), the dose response model was found to be more suitable due to its ability to overcome convergence issues. The spread of N successive waves has also been described as multiphase percolation with a period of pandemic relaxation between two successive waves.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
