https://doi.org/10.1140/epjp/s13360-023-03961-y
Regular Article
Numerical model of hepatic glycogen phosphorylase regulation by nonlinear interdependent dynamics of calcium and 
Department of Mathematics and Humanities, SVNIT, Ichchhanath, 395007, Surat, Gujarat, India
Received:
17
October
2022
Accepted:
7
April
2023
Published online:
9
May
2023
The liver’s primary function is to integrate various signals to retain stable blood glucose levels. Glycogenolysis, gluconeogenesis, and other metabolic processes are regulated by circulating hormones via calcium-dependent signaling. In this paper, the influence of calcium concentration on glycogen phosphorylase in hepatocytes is investigated utilizing a numerical approach. The system comprising two nonlinear reaction-diffusion equations for calcium and , respectively, has been coupled to propose a mathematical model. The temporal equation of the fraction of active glycogen phosphorylase (
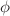) is also incorporated into the model. The finite volume and the Crank Nicolson methods are implemented along spatial and temporal dimensions, while the Gauss-Seidel method is employed to simplify the resulting nonlinear equations. The impact of calcium influx, EGTA buffer concentration, SERCA pump rate constant, and leak flux constant on the 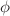has been studied. It has been observed that interdependent calcium and dynamics have a crucial role in controlling the blood glucose level. Any dysregulation of calcium and processes can lead to the dysregulation of glycogen phosphorylase. This may lead to hyperglycemia or hypoglycemia.
Yogita Jagtap and Neeru Adlakha have contributed equally to this work.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
