Eur. Phys. J. Plus (2022) 137: 1265
https://doi.org/10.1140/epjp/s13360-022-03472-2

Regular Article

Can we bypass no-go theorem for Ricci-inverse gravity?

¹ UM-DAE Centre for Excellence in Basic Sciences, 400098, Mumbai, India
² Department of Physics, Indian Institute of Technology Bombay, 400076, Mumbai, India

^b josephpj@iitb.ac.in

Received: 13 April 2022
Accepted: 7 November 2022
Published online: 21 November 2022

Abstract

Recently, Amendola et al. proposed a geometrical theory of gravity containing higher-order derivative terms (Amendola et al. in Phys Lett B 811:135923, 2020. https://doi.org/10.1016/j.physletb.2020.135923, arXiv:2006.04209). The authors introduced anticurvature scalar (A), which is the trace of the inverse of the Ricci tensor (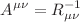$A^{\mu \nu }=R_{\mu \nu }^{-1}$). In this work, we consider two classes of Ricci-inverse—Class I and Class II—models. Class I models are of the form f(R, A) where f is a function of Ricci and anticurvature scalars. 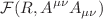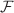Class II models are of the form $\mathcal{F}(R,A^{\mu \nu }{A}_{\mu \nu })$ where $\mathcal{F}$ is a function of Ricci scalar and square of anticurvature tensor. For both these classes of models, we numerically solve the modified Friedmann equations in the redshift range $1500<z<0$. We show that the late-time evolution of the Universe, i.e., evolution from matter-dominated epoch to accelerated expansion epoch, can not be explained by these two classes of models. Using the reduced action approach, we show that we can not bypass the no-go theorem for Ricci-inverse gravity models. Finally, we discuss the implications of our analysis for the early-Universe cosmology.