https://doi.org/10.1140/epjp/s13360-022-02486-0
Regular Article
Analytic derivation of the nonlinear gluon distribution function
Department of Physics, Razi University, 67149, Kermanshah, Iran
a grboroun@gmail.com, boroun@razi.ac.ir
Received:
18
September
2021
Accepted:
14
February
2022
Published online:
22
February
2022
In the present article, two analytical solutions based on the Laplace transforms method for the linear and nonlinear gluon distribution functions have been presented at low values of x. These linear and nonlinear methods are presented based on the solutions of the Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) evolution equation and the Gribov–Levin–Ryskin–Mueller–Qiu (GLR-MQ) equation at the leading-order accuracy in perturbative QCD, respectively. The gluon distributions are obtained directly in terms of the parameterization of structure function 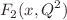 and its derivative and compared with the results from the parameterization models. The
and its derivative and compared with the results from the parameterization models. The  changes at the threshold are considered in the numerical results. The effects of the nonlinear corrections are visible as
changes at the threshold are considered in the numerical results. The effects of the nonlinear corrections are visible as  decreases and vanish as
decreases and vanish as  increases. The nonlinear corrections tame the behavior of the gluon distribution function at low x and
increases. The nonlinear corrections tame the behavior of the gluon distribution function at low x and  in comparison with the parameterization models.
in comparison with the parameterization models.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2022




