Eur. Phys. J. Plus (2022) 137: 225
https://doi.org/10.1140/epjp/s13360-022-02444-w

Regular Article

Generalized semiconfined harmonic oscillator model with a position-dependent effective mass

Physique Nucléaire Théorique et Physique Mathématique, Université Libre de Bruxelles, Campus de la Plaine CP229, B-1050, Boulevard du Triomphe, Brussels, Belgium

^a Christiane.Quesne@ulb.be

Received: 19 October 2021
Accepted: 2 February 2022
Published online: 12 February 2022

Abstract

By using a point canonical transformation starting from the constant-mass Schrödinger equation for the isotonic potential, it is shown that a semiconfined harmonic oscillator model with a position-dependent mass in the BenDaniel–Duke setting and the same spectrum as the standard harmonic oscillator can be easily constructed and extended to a semiconfined shifted harmonic oscillator, which could result from the presence of a uniform gravitational field. A further generalization is proposed by considering a m-dependent position-dependent mass for 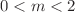$0<m<2$ and deriving the associated semiconfined potential. This results in a family of position-dependent mass and potential pairs, to which the original pair belongs as it corresponds to 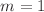$m=1$. Finally, the potential that would result from a general von Roos kinetic energy operator is presented and the examples of the Zhu–Kroemer and Mustafa–Mazharimousavi settings are briefly discussed.