Role of quasi-homologous condition to study complex systems in gravity

M. Z. Bhatti; Z. Yousaf; S. Khan

doi:10.1140/epjp/s13360-021-01889-9

EPJ

a
b
c
d
e
ap
st
h
plus
ds
pv
ti
qt
am
n

2024 Impact factor 2.9

EPJ PLUS - Condensed Matter and Complex Systems

Eur. Phys. J. Plus (2021) 136: 975
https://doi.org/10.1140/epjp/s13360-021-01889-9

Regular Article

Role of quasi-homologous condition to study complex systems in 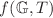$f (G, T)$ $f({\mathbb {G}}, T)$ gravity

M. Z. Bhatti^a, Z. Yousaf and S. Khan

Department of Mathematics, University of the Punjab, Quaid-i-Azam Campus, 54590, Lahore, Pakistan

^a mzaeem.math@pu.edu.pk

Received: 15 July 2021
Accepted: 19 August 2021
Published online: 27 September 2021

Abstract

We study the notion of complexity for dynamical self-gravitating (dissipating as well as non-dissipating) structures with anisotropic fluid configuration, under 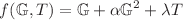$f (G, T) = G + α G^{2} + λ T$ $f({\mathbb {G}}, T)={\mathbb {G}}+\alpha {\mathbb {G}}^{2}+\lambda T$ gravitational model. Here, $G$ ${\mathbb {G}}$ and T symbolize the Gauss–Bonnet invariant and trace of the stress-energy tensor, respectively. 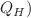To address the evolution of the dynamical celestial body, we impose two conditions on the system, i.e., the quasi-homologous (i.e., $Q_{H})$ $Q_{H})$ condition and zero complexity factor 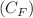$(C_{F})$ $(C_{F})$ condition. Under the above-mentioned conditions, different solutions to the 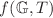$f (G, T)$ $f({\mathbb {G}}, T)$ gravitational equations are proposed. Some of the given theoretical models illustrate the evolution of non-static structure in which the center ( 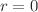$r = 0$ $$r=0$$ ) of the system is enclosed by a void, while some of them characterize the dissipative anisotropic matter configurations in which the fluid fills up the entire system. Few of the stellar models fulfill the Israel junction conditions, while others satisfy the Darmois matching conditions.