Eur. Phys. J. Plus (2021) 136: 881
https://doi.org/10.1140/epjp/s13360-021-01878-y

Regular Article

On the topological and crosscap entropies in non-oriented RCFTs

¹ Departamento de Física, Centro de Investigación y de Estudios Avanzados del IPN, P.O. Box 14-740, CP. 07000, México City, Mexico
² División de Ciencias Exactas, Naturales y Tecnológicas, Centro Universitario del Sur, Universidad de Guadalajara, Enrique Arreola Silva No. 883, Centro, 49000, Cd Guzman, Jal, Mexico

^a compean@fis.cinvestav.mx

Received: 23 June 2021
Accepted: 16 August 2021
Published online: 26 August 2021

Abstract

We establish a relation between the boundary and the topological entropies for the conformal minimal models in some of the simplest models of the unitary A–A series. We show that in these models the boundary entropy is a difference of topological entropies. Furthermore, we define the crosscap entropy as the analog to the boundary entropy in non-oriented theories. The crosscap entropy is defined as the logarithm of the degeneracy of the ground state due to the presence of crosscaps, and it can be expressed in terms of the crosscap coefficients. This crosscap entropy has not an explicit relation to the topological entropy as the boundary entropy. However, we propose a new quantity, 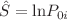$\widehat{S}=\text{ln}{P}_{0i}$ defined in terms of the modular transformation P between the open and closed channel of the Möbius partition function. With this quantity, the crosscap entropy can be regarded as a difference of entropies, very similar to the boundary entropy. We also compute the left-right entanglement entropy (LREE) for crosscap states, and we express it in terms of 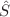$\widehat{S}$. An explicit example of the LREE of the crosscap state in Wess–Zumino–Witten is carried out.