Eur. Phys. J. Plus (2021) 136: 1060
https://doi.org/10.1140/epjp/s13360-021-02057-9

Regular Article

Shannon entropies of asymmetric multiple quantum well systems with a constant total length

¹ Centro de Investigación en Computación, Instituto Politécnico Nacional, UPALM, CDMX, 07738, Mexico City, Mexico
² Catedrática CONACyT, Centro de Investigación en Computación, Instituto Politécnico Nacional, UPALM, CDMX, 07738, Mexico City, Mexico
³ Department of Physics, Faculty of Science, Qom University of Technology, Qom, Iran
⁴ Huzhou University, 313000, Huzhou, China
⁵ Laboratorio de Información Cuántica, CIDETEC, Instituto Politécnico Nacional, UPALM, CDMX, 07700, Mexico City, Mexico

^c sunghdb@yahoo.com
^e dongsh2@yahoo.com

Received: 29 September 2021
Accepted: 9 October 2021
Published online: 21 October 2021

Abstract

We calculate the Shannon entropies numerically for a rectangular asymmetric multiple quantum well system with a constant total length. This quantum system is designed as an asymmetric multiple well with equal barriers but unequal arithmetic sequence (AS) wells. We show how the number of wells and confining potential depth affect the Shannon entropy density and the Shannon entropy. When increasing the confined potential depth 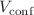$V_{\mathrm{conf}}$, the magnitude of the position entropy density decreases while that of the momentum entropy density increases, but there is a very slight difference when the confined potential depth reaches a large value. Also, the oscillation frequency of the position entropy density inside the quantum barriers decreases while that of the position entropy density inside the quantum wells increases. When the potential well depth reaches a large value, the moving particle is mainly confined in a relatively wide potential well, and the position entropy density disappears in other barriers and potential wells. As the number of wells increases, the oscillation frequency of the position entropy density decreases inside the barriers but increases inside the quantum wells. 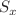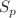It is very interesting to see that the $S_x$ and $S_p$ do not always decrease or increase monotonically with the confined potential depth 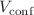$V_{\mathrm{conf}}$, but their sum always satisfies the BBM inequality.