Eur. Phys. J. Plus (2021) 136: 673
https://doi.org/10.1140/epjp/s13360-021-01636-0

Regular Article

The Schrödinger particle on the half-line with an attractive $\delta$-interaction: bound states and resonances

¹ Department of Higher Mathematics, ITMO University, S. Petersburg, Russian Federation
² Dipartimento di Scienze Ingegneristiche, Univ. degli Studi Guglielmo Marconi, Via Plinio 44, 00193, Rome, Italy
³ CERFIM, PO Box 1132, Locarno, 6601, Switzerland
⁴ Departamento de Física Teórica, Atómica y Óptica, and IMUVA, U. de Valladolid, 47011, Valladolid, Spain

^c luismiguel.nieto.calzada@uva.es

Received: 23 March 2021
Accepted: 1 June 2021
Published online: 18 June 2021

Abstract

In this paper, we provide a detailed description of the eigenvalue 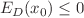$E_D(x_0)\le 0$ (respectively, 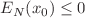$E_N(x_0)\le 0$) of the self-adjoint Hamiltonian operator representing the negative Laplacian on the positive half-line with a Dirichlet (resp. Neuman) boundary condition at the origin perturbed by an attractive Dirac distribution 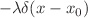$-\lambda \delta (x-x_0)$ for any fixed value of the magnitude of the coupling constant. We also investigate the 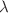$\lambda$-dependence of both eigenvalues for any fixed value of 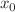$x_0$. Furthermore, we show that both systems exhibit resonances as poles of the analytic continuation of the resolvent. These results will be connected with the study of the ground state energy of two remarkable three-dimensional self-adjoint operators, studied in depth in Albeverio’s et al. monograph, perturbed by an attractive $\delta$-distribution supported on the spherical shell of radius $r_0$.