Eur. Phys. J. Plus (2017) 132: 352
https://doi.org/10.1140/epjp/i2017-11613-7

Regular Article

A singular one-dimensional bound state problem and its degeneracies

¹ Department of Mathematics, İzmir Institute of Technology, Urla, 35430, İzmir, Turkey
² Departamento de Física Teórica, Atómica y Óptica, IMUVA. Universidad de Valladolid, Campus Miguel Delibes, Paseo Belén 7, 47011, Valladolid, Spain
³ Department of Mathematics, İstanbul Bilgi University, Dolapdere Campus 34440 Beyoğlu, İstanbul, Turkey
⁴ Department of Physics, Adnan Menderes University, 09100, Aydın, Turkey

^* e-mail: fatih.erman@gmail.com

Received: 29 March 2017
Accepted: 27 June 2017
Published online: 14 August 2017

Abstract

We give a brief exposition of the formulation of the bound state problem for the one-dimensional system of N attractive Dirac delta potentials, as an 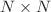matrix eigenvalue problem (). The main aim of this paper is to illustrate that the non-degeneracy theorem in one dimension breaks down for the equidistantly distributed Dirac delta potential, where the matrix 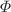becomes a special form of the circulant matrix. We then give elementary proof that the ground state is always non-degenerate and the associated wave function may be chosen to be positive by using the Perron-Frobenius theorem. We also prove that removing a single center from the system of N delta centers shifts all the bound state energy levels upward as a simple consequence of the Cauchy interlacing theorem.