Eur. Phys. J. Plus (2021) 136: 416
https://doi.org/10.1140/epjp/s13360-021-01376-1

Regular Article

Rogue wave signals in a coupled anharmonic network: effects of the transverse direction

¹ Unité de Recherche de Mécanique et de Modélisation des Systèmes Physiques (UR-2MSP), Faculté des Sciences, Université de Dschang, BP 69, Dschang, Cameroun
² Unité de Recherche de Matière Condensée, d’Electronique et de Traitement du Signal (UR-MACETS), Faculté des Sciences, Université de Dschang, BP 67, Dschang, Cameroun

^b fbpelap@yahoo.fr

Received: 27 August 2020
Accepted: 29 March 2021
Published online: 20 April 2021

Abstract

In this paper, we consider the dynamics of modulated waves in a nonlinear two-dimensional discrete electrical lattice made of several well-known anharmonic modified Noguchi lines coupled transversely to one another with a linear inductor. In the linear limit and depending on the chosen frequency domain, we demonstrate that the network behaves either as a right-handed line or as a left-handed line. We also establish that the band pass character of the modified Noguchi line increases the bandwidth of the allowed frequencies for which the system adopts the left-handed behavior. Based on the reductive perturbation method in the semi-discrete approximation, we derive a (2 + 1)-dimensional nonlinear Schrodinger (2D-NLS) equation governing the dynamics of the small amplitude signals in the system. The specific nature of this amplitude equation is examined, and it appears that its hyperbolic or elliptic character strongly depends on the coupling inductor $L_2$. Moreover, using a simple transformation, we reduce the obtained equation to a (1 + 1)-dimensional nonlinear Schrodinger equation (1D-NLS). The exact first- and second-order rogue wave’s solutions of this 2D-NLS equation are derived in bandwidth frequencies where the network may exhibit modulational instability. The results of our investigations display number of interesting rogue wave profiles which have not been observed in the scientific literature. 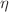Furthermore, we examine the effects of both the coupling linear inductor $L_2$ and the nonlinear dispersion factor $\eta$ on the characteristics of the rogue waves and also on their propagation through the network. 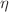It appears that $L_2$ and $\eta$ can be used to squeeze or stretch the shape of the rogue waves signals traveling in the network. These numerical results are in perfect agreement with the analytical predictions.