https://doi.org/10.1140/epjp/s13360-020-00994-5
Regular Article
Fractal-fractional order dynamical behavior of an HIV/AIDS epidemic mathematical model
1
School of Engineering, Monash University Malaysia, 47500, Subang Jaya, Selangor, Malaysia
2
Department of Mathematics, University of Malakand, Dir(L), 18000, Khyber Pakhtunkhwa, Pakistan
3
Department of Information Technology, School of Science and Engineering, Malaysia University of Science and Technology, 47810, Petaling Jaya, Selangor, Malaysia
b faranak.rabiei@monash.edu, faranak.rabiei@gmail.com
Received:
24
July
2020
Accepted:
8
December
2020
Published online:
4
January
2021
In this manuscript, an HIV/AIDS epidemic model including five compartments of 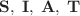 and
and  is proposed under fractal-fractional-order derivative. The existence theory utilizing Schaefer- and Banach-type fixed point theorems for the solution of considered model is constructed. Additionally, Ulam–Hyers
is proposed under fractal-fractional-order derivative. The existence theory utilizing Schaefer- and Banach-type fixed point theorems for the solution of considered model is constructed. Additionally, Ulam–Hyers  and generalized
and generalized  stability conditions via nonlinear functional analysis are established. A fractional type of two-step Lagrange polynomial known as fractional Adams–Bashforth (AB) method is developed for numerical simulation of the considered model. The simulated results for various fractal-fractional orders are tested on some existing real data of disease spread in South Africa and show that the values of
stability conditions via nonlinear functional analysis are established. A fractional type of two-step Lagrange polynomial known as fractional Adams–Bashforth (AB) method is developed for numerical simulation of the considered model. The simulated results for various fractal-fractional orders are tested on some existing real data of disease spread in South Africa and show that the values of 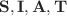 are decreased after treatment was started. In addition,
are decreased after treatment was started. In addition,  , the population of infected people who have changed their sexual habits sufficiently after starting the treatment and changing their sexual behavior, increased gradually. Finally, it is shown that for all five compartments of the proposed model of HIV/AIDS, the smaller values of fractal-fractional order have better performance than larger values.
, the population of infected people who have changed their sexual habits sufficiently after starting the treatment and changing their sexual behavior, increased gradually. Finally, it is shown that for all five compartments of the proposed model of HIV/AIDS, the smaller values of fractal-fractional order have better performance than larger values.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2021




